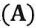109 年 - [無官方正解]109 國立中山大學_碩士班招生考試_電機(甲、戊、己組)、通訊所(乙組)、電波聯合：工程數學甲#106080　

1.微分方程式 為非線性方程式。
(A)是
(B)否

2.微分方程式 有三個平衡點。
(A)是
(B)否

3.微分方程式 的解,不管初值為何,都會收斂到0。
(A)是
(B)否

5.令函數y(t)的拉普拉斯轉换為Y(s)·則函數 的拉普拉斯轉换為s²Y(s)。
(A)是
(B)否

6.函數 的傅立葉轉換(Fourier transform)為
(A)是
(B)否

9. 定義Del操作子為: 。若為具有連續一二偏導函數的連續純量場函數,則x(Vφ)≠0除非φ是常數函數或線性函數。
(A)是
(B)否

11.假設u(t)≡0, 。下列哪一組初值 所對應的解不是z(t)≡0, 。
(A)(0,0)
(B)(π,0)
(C)(0,π)
(D)(0,一π)

12.假設u(t)≡, 。將前述方程式就 線性化後之線性方程式,滿足以下哪個敘述?
(A)若b=0,則任何初值對應的解皆會收斂到0。
(B)若b=0,則有些初值對應的解皆會發散。
(C)若b=1,則任何初值對應的解皆會收斂到0。
(D)若b=-1,則有些初值對應的解皆會收斂到0。

13.假設u(t)≡0, 。將前述方程式就 線性化後之線性方程式,滿足以下哪個敘述?
(A)若b=0,則有些初值對應的解皆會收斂到0。
(B)若b=0,則任何初值對應的解皆會收斂到0。
(C)若b=1,則任何初值對應的解皆會收斂到。
(D)若b=1,則任何初值對應的解皆會發散。

14.考慮將前述方程式就 線性化後之線性方程式。假設b=0,且該方程式之輸入項(forcing term)為單位步階函數。下列敘述何者為正確?
(A)該線性方程式的解會收斂到1。
(B)如該線性方程式的初值為(1,0),則方程式的解為sin t。
(C)該線性方程式的解會發斂
(D)該線性方程式的解會不斷。

15.考慮將前述方程式就 線性化後之線性方程式。假設b=2,且該方程式之输入項(forcing trm)為sin t。下列敘述何者為正確?
(A)該線性方程式的解會收斂到一 cost。
(B)該線性方程式的解會收斂到 sint。
(C)如該線性方程式的初值為(0,0),則方程式的解為sin t。
(D)如該線性方程式的初值為(0,1),則方程式的解為cos t。

17.令 。下列關於 之敘述何者正確? 
(A)該矩陣是一個3x3的方陣。
(B)該矩陣在t≥0时,永為一個可逆矩陣。
(C)該矩陣(3,2)位置那一項為 。
(D)該矩陣(1,2)置那一項為 。
(E)當t→∞時,該矩陣收斂為0矩陣。

18. Consider the linear equation Ax = b, where A = [a₁, a₂, a₃, a₄ ] ∈ 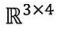and a₁, a₂, a₃, a₄ are column vectors of A. Suppose a₁ + a₂ + a₃ + a₄ = b. Which of the following statements are true?
(A) The linear equation has exactly one solution.
(B) The linear equation has infinitely many solutions.
(C) No conclusion can be drawn about the number of solutions to the linear equation.
(D) The vectors a₁, a₂,a₃, a₄ are linearly dependent.
(E) rank([A,b]) = rank

19. Consider the linear equation Ax = b with A ∈ . Which of the following statements are true?
(A) If rank = m, then there exists at least one solution.
(B) If rank = n, then there exists exactly one solution.
(C) Ifrank = n, then the column vectors of A are linearly independent.
(D) Ifn ＞ m, then there exists at least one solution.
(E) Ifm ＞ n, then there exists at most one solution.

20.Consider the linear mapping L:V - W. Let be the zero vectors in V and W, respectively. Which of the following statements are true?
(A) The condition L(V₁) = L(V₂) implies V₁ = V₂.
(B) For any w ∈ W, there exists v ∈ V such that L(V) = W.
(C) If L is one-to-one, then L(V) = impliesv =
(D) IfV₁,V₂,..., are linearly independent, L(V₁), L(V₂),.., are also linearly independent.
(E) The condition G₁V₁:+C₂V₂+...+ = implies c₁L(V₁)+c₂L(V₂)+⋯..+ =

21. Given vectors x, y, z in IR" and matrices A, B, C in . Which of the following statements are true?
(A)

(B)

(C) (A+B)(A -B) = A² -B² 

(D) If AC = BC and C is not the zero matrix, then A = B.
(E) If AB equals the zero matrix, then BA also equals the zero matrix.

22.Let A ∈ , denote the column space of A, denote the null space of A,
and dim(S) denote the dimension of a subspace S. Which of the following statements are true?

(A) For any x ∈ , there exists u∈ and v ∈  such that x = u + v.

(B) Suppose u ∈ and v ∈ . Then = 0.

(C) dim + dim = n

(D) For any y ∈ , there exists x ∈ such that y = .

(E) Ify ∈   , then y is the zero vector in .

23. Let A ∈ and x ∈ . Which of the following statements are true?

(A) If A is singular, then O is an eigenvalue of A.

(B) A and share the same eigenvalues and eigenvectors.

(C) If A is diagonalizable, then A has n distinct eigenvalues.

(D) Suppose that A is nonsingular. The condition Ax = λx implies .

(E) Suppose that all the eigenvalues of A are real and positive. Then we have ＞ 0.