試題詳解

9. 有一個抽牌拿獎金活動，規則如下 ：
在一個不透明箱子中 有 2 張標示金額 「 1000 元 」 的牌及3張標示金額 「 0 元 」 的牌。參加者從箱中隨機抽出一張牌，在不知道抽出牌標示的金額情況下，主持人再將一張標示金額「500 元」的牌放入箱中。此時參加者有以下兩種選擇：
( 一 ) 保留原先抽出的牌 ， 該牌標示的金額即為獲得的獎金 。
( 二 ) 放棄原先抽出的牌 且不放回，再從箱中隨機抽出一張牌，該牌標示的金額
即為獲得的獎金 。
今某甲參加此活動 ， 假設每張牌被抽中的機會均相等，試選出正確的選項 。
(A) 若某甲選擇 ( 一 )， 則獲得獎金0 元的機率為
(B) 若某甲選擇 ( 一 )， 則獲得獎金 的 期 望值為500元
(C) 若某甲選擇 ( 二 )， 則獲得獎金1000元的機率為
(D)若某甲選 擇 ( 二 )， 則獲得獎金0元的機率為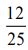
(E) 若某甲選擇 ( 二 )， 則獲得獎金的期望值 為 420 元