題組內容
1. We have the following definitions and theorem related to NP-completeness.
Definition 1. Let X1 and X2 be tow problems. X1 polynomially reduces to X2 (written as 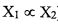 ) if and only if X1can be solved in polynomial time, by using a polynomial time algorithm which solves X2.
) if and only if X1can be solved in polynomial time, by using a polynomial time algorithm which solves X2.
Definition 2. A problem is said to be a P (resp, NP) problem if it can be solved in polynomial time by a deterministic (resp,, non-deterministio) algorithn.
Definition 3. NP (resp., P) is the set of all NP (resp., P) problems.
Definition 4. A problem X is an NP-complete (NPC) problem if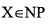 and every NP problem reduces to X.
and every NP problem reduces to X.
Cook's Theorem. NP=P if and only if the satisfiability (SAT) problem is a P problem. (This implies that every NP problem polynomially reduces to SAT.)
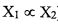 ) if and only if X1can be solved in polynomial time, by using a polynomial time algorithm which solves X2.
) if and only if X1can be solved in polynomial time, by using a polynomial time algorithm which solves X2. Definition 2. A problem is said to be a P (resp, NP) problem if it can be solved in polynomial time by a deterministic (resp,, non-deterministio) algorithn.
Definition 3. NP (resp., P) is the set of all NP (resp., P) problems.
Definition 4. A problem X is an NP-complete (NPC) problem if
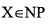 and every NP problem reduces to X.
and every NP problem reduces to X.Cook's Theorem. NP=P if and only if the satisfiability (SAT) problem is a P problem. (This implies that every NP problem polynomially reduces to SAT.)
(A) (15%) Assume that  By the assumptions and above definition and theorem, prove that D is NP-complete.
By the assumptions and above definition and theorem, prove that D is NP-complete.