申論題

8. It is given grad f = ∇f = 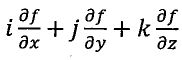, div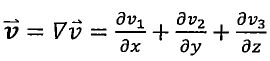, and curl 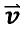 =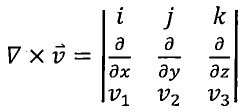, where f and v₁, v₂ and v₃ are the scalar functions of x, y and z.
(i) ∇ × (∇f) = 0   (2)
states "Gradient fields are irrotational. That is, if a continuously differentiable vector function is the gradient of a scalar function f, then its curl is a zero vector." 

(ii) ∇ ⋅ (∇ × v) = 0 (3)

states "the divergence of the curl of a twice continuously differentiable vector function v is zero.”

(a) (6%), (6%) Please first prove Equations (2) and (3), respectively