申論題

12. Given a connected and weighted graph G = (V, E), where all the edge weights are positive integers. The eccentricity is the greatest shortest path distance between v and any other vertex. That is, 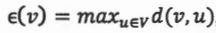, where d(v,u) denotes the shortest path distance between vertices v and u. For example, in the following figure, 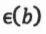= max{d[b,a],d(b,c),d(b,d)} =9. Please answer the following questions.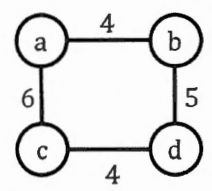

(b) (2 x 3 points) In contrast to the center, which must be a vertex, an absolute center is a point that can be on an edge or on a vertex, such that its maximum sbortest path distance to all vertices is minimum. Take the following graph as an example, the point x is an absolute center, because the shortest path distances from x to vertices a, b, c, d are 6.5, 2.5, 6.5, 2.5, respectively. That is, the maximum sbortest path distance from x to all the other vertices is 6.5, which is minimum among all possible cases.
  
Given the definition of the absolute center, we know that there may be multiple absolute centers in a graph. So, please answer the following questions. (b-i) If there are multiple absolute centers in a graph, can all of them be on vertices, i.e, no absolute center is on an edge? If yes, please provide an example; If no, please provide a proof. (b-ii) If there are multiple absolute centers in a graph, can some of them be on vertices, and some of them be on edges at the same time? If yes, please provide an example; If no, please provide a proof.