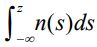申論題

(五)承上(四)，在 1 日之內發生 2 件或 2 件以上事故的機率為何？（答案不 用寫出數字，但要使用所附提示函數符號） 。（4 分） 提示：
● 卜瓦松（Poisson）分布函數= p（發生次數：n, 發生次數期望值：λ）=

● 卜瓦松累積分布函數= Po（發生次數：n, 發生次數期望值：λ）=

●指數（exponential）分布函數= e（變數：x, 1/期望值：λ）=λe^-λ 
●指數（exponential）累積分布函數= E（變數：x, 1/期望值：λ）= 1-λe^-λ 
●二項（binomial）分布函數 b（發生次數：n, 觀察次數：N，發生機率：p）=

●二項累積分布函數 B（發生次數：n, 觀察次數：N, 發生機率：p）=

●標準常態（normal）分布函數 n( z ) =

●標準常態累積分布函數 N ( z ) =