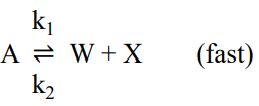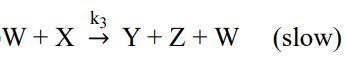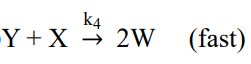申論題

       The steady state approximation,occasionally called the stationary-state approximation or Bodenstein's quasi-steady state approximation, involves setting the rate of change of a reaction intermediate in a reaction mechanism equal to zero so that the kinetic equations can be simplified by setting the rate of formation of the intermediate equal to the rate of its destruction.

       In practice it is sufficient that the rates of formation and destruction are approximately equal, which means that the net rate of variation of the concentration of the intermediate is small compared to the formation and destruction, and the concentration of the intermediate varies only slowly, similar to the reactants and products. 

       Its use facilitates the resolution of the differential equations that arise from rate equations, which lack an analytical solution for most mechanisms beyond the simplest ones. The steady state approximation is applied, for example, in Michaelis-Menten kinetics.

      As an example, the steady state approximation will be applied to two consecutive, irreversible, homogeneous first order reactions in a closed system. This model corresponds, for example, to a series of nuclear decompositions like
²³⁹U → ²³⁹Np → ²³⁹Pu.

已知氣體 A 分子可進行分解反應，其反應機構如下：
①
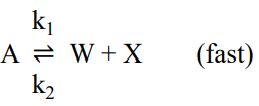
②
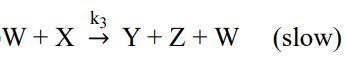
③

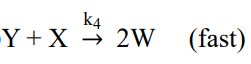
(1)若該反應的速率定律式可寫成r_A = k[A] ^m，試以穩態假設推導出 k 值以及 m 值 (需有計算過程)。(2 分)