阿摩線上測驗
題組內容
4.(26%)下面的問題共有四個子题,只要簡短扼要地回答提問即可,不須寫出答案背後的推導。
Let V be a vector space with dim(V) = n and an ordered basis E := [x1,... .,xn].Let
Let V be a vector space with dim(V) = n and an ordered basis E := [x1,... .,xn].Let
F:=[y1 , Yn] be the ordered orthonormal basis generated from basis E by applying the Gram- Schmidt Orthogonalization Process. For any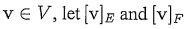
denote the coordinate vectors of v with respect to bases E and F, respectively. Let T denote the transition matrix from basis E to basis F. Let L :
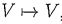, i.e. L is a linear operator mapping V into itself, and suppose that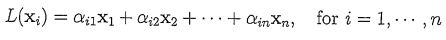
Let's denote the matrix representation of L with respect to basis E by A.
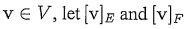denote the coordinate vectors of v with respect to bases E and F, respectively. Let T denote the transition matrix from basis E to basis F. Let L :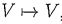, i.e. L is a linear operator mapping V into itself, and suppose that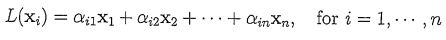Let's denote the matrix representation of L with respect to basis E by A.
(c) (6%) Suppose now that 
and denote X := [x1,... ,xn].Let X = QR be the QR factorization of matrix X. Is there any relationship between matrices T, Q and R? If yes, write an equation to describe such a relationship. If no, give a brief explanation for it.