題組內容
Let X and Y be continuous randoun variables with the joint probability density function
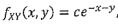 , 0 ≤x<ㆀ,0≤y<∞, where c is a constant. Then c= (a)
, 0 ≤x<ㆀ,0≤y<∞, where c is a constant. Then c= (a)
E(XY2)= (b) ,and cov(X,Y)= (c) . Given the information that X = x, the
conditional probability density function of Y is 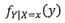 = (d) . Now we let Z = X+Y
= (d) . Now we let Z = X+Y
with 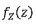 the probability density function and.
the probability density function and. 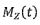 the corresponding mnoment generating function.Then
the corresponding mnoment generating function.Then 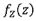 = (e) and My(t) = (f) .
= (e) and My(t) = (f) .