申論題

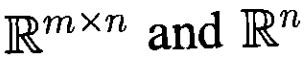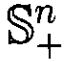Problem 3. (25 %) Let denote the set of real m x n matrices and the set of real n x 1 column vectors, respectively, and let denote the set of real n x n symmetric positive semidefinite (PSD) matrices. This problem includes two parts as follows:

(ii) (10 %) Suppose that A,
and Tr(A) denotes the trace of A (i.e., the sum of all the diagonal elements of A).
(1)Is Tr(AX)≥0 true?
(2)Is it true that if Tr(AX) = 0, then(zero matrix)?
Prove or disprove your answer.