今日錯題測驗-國中會考基測◆數學科-阿摩線上測驗
Abc Tse剛剛做了阿摩測驗,考了35分
15. 圖 ( 七 ) 為一直角柱,其底面是三邊長為 5、 12、 13 的
直角三角形。若下列選項中的圖形均由三個矩形與兩個
直角三角形組合而成,且其中一個為圖 ( 七 ) 的直角柱
的展開圖,則根據圖形中標示的邊長與直角記號判斷,
此展開圖為何? 

24. 圖 ( 十七 ) 表示 A 、 B 、 C 、 D 四點在圓 O 上的
位置,其中 AD = 180° , 且 AB = BD , BC = CD。
若阿超在 AB 上取一點 P ,在 BD 上取一點 Q ,
使得 ∠APQ = 130°
,則下列敘述何者正確?

(A) Q 點在 BC 上,且 BQ > QC
(B) Q 點在 BC 上,且 BQ < QC
(C) Q 點在 CD 上,且 CQ > QD
(D) Q 點在 CD 上,且 CQ < QD
17. 圖 ( 八 ) 為兩直線 L、M 與 ∆ABC 相交的情形,其中
L、M 分別與  平行。根據圖中標示的角度,
求 ∠B 的度數為何?
平行。根據圖中標示的角度,
求 ∠B 的度數為何?

(A) 55
(B) 60
(C) 65
(D) 70
請閱讀下列敘述後,回答 24 ~ 25 題
表(一)、表(二)呈現 PA、PB 兩種日光燈管的相關數據,其中光通量用來衡量
日光燈管的明亮程度。 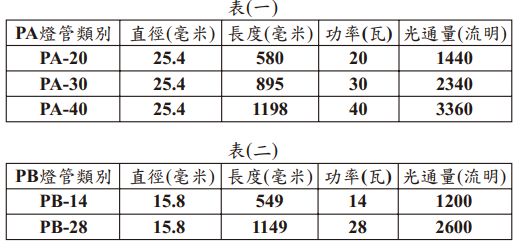
今日錯題測驗-國中會考基測◆數學科-阿摩線上測驗
Abc Tse剛剛做了阿摩測驗,考了35分
This is a large modal.