活動名稱
【解題達人! We want you!】
活動說明
阿摩站上可謂臥虎藏龍，阿摩發出200萬顆鑽石號召達人們來解題! 針對一些題目可能有疑問但卻缺少討論，阿摩主動幫大家尋找最佳解! 懸賞試題多達20萬題，快看看是否有自己拿手的科目試題，一旦你的回應被選為最佳解，一題即可獲得10顆鑽石。 懸賞時間結束後，只要摩友觀看你的詳解，每次也會得到10顆鑽石喔!
關於鑽石
如何使用:

  • ✔懸賞試題詳解
  • ✔購買私人筆記
  • ✔購買懸賞詳解
  • ✔兌換VIP
    (1000顆鑽石可換30天VIP)
  • ✔兌換現金
    (50000顆鑽石可換NT$4,000)
如何獲得:

  • ✔解答懸賞題目並被選為最佳解
  • ✔撰寫私人筆記販售
  • ✔撰寫詳解販售(必須超過10讚)
  • ✔直接購買 (至站內商城選購)
如何兌換現金:

** 所有鑽石收入，都會有10%的手續費用

近期考題

考題每隔30分鐘持續更新
【非選題】
二、工程契約履約期間，機關得視案件性質及實際需要指派工程司駐場，代表機關監督 廠商履行契約各項應辦事項。一般而言，有那些職權機關會授與工程司？（15 分）



119. 下列何項行為已違反傳染病防治法？
(A)傳染病病人依主管機關通知於指定 隔離治療機構施行隔離治療
(B)旅館或店鋪之負責人發現疑似傳染病病人或其屍體，未經醫師診斷或檢驗者，於 24 小時內通知當地主管機關
(C)為了提高臉書觸及率，散布聳動的疫情謠言或傳播不實疫情消息
(D)主動清除病媒孳生源 。



【非選題】
七、試述下列情況係於那一法令中規範。（每小題 2 分，共 12 分）

【題組】 (1)醫事人員名稱專用之規範（請任舉兩類醫事人員）。



【非選題】
三、依據111年3月6日內政部消防署訂頒消防人員救災安全手冊第15章搶救地 下空間（場域）火災安全指導原則，詳述進入搶救地下空間前的安全注意事項。（25分）



【非選題】
二、運往國外修理、裝配之貨物，復運進口者，若欲以其修理、裝配所需之費用作為完 稅價格課徵關稅，則：

【題組】⑴ 貨物出口及復運進口時，應如何申報？（5 分）



【非選題】
6.(13 分） 假設某二元樹上各節點資料爲一英文字母，已知此二元樹中序追蹤所得字串爲CDAEB -其後序 追蹤所得字串爲DCEBA。

【題組】 (a) (8分）請畫出此二元樹。



【非選題】
三、請試述下列名詞之意涵：（每小題 5 分，共 20 分）

【題組】(三)移情關係（transference relationship）



【非選題】
二、技職教育的本質與目標是什麼？我國為何要實施產學合作？試提出強化我國技職教 育產學合作的創新措施。（25 分）



4. 何者為使用「有鎖」接頭(keyed connectors)的理由？
(A) 阻止非授權人員使用
(B) 減少插接錯誤的機會
(C) 具有更高的電流容量
(D) 以上皆是



【非選題】

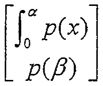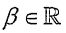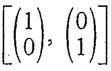4.(25%) Let P2 denote the vector space of all polynomials of degree less than 2. (Consider the transformation L:P2 →R2 defined by L(p(x)): =630834c1d2f7f.jpg with  undecided parameters a＞0 and 630834e82b49e.jpg . Let A be the matrix representation of transformation L with respect to the ordered bases E = [I, x] and E'= 6308350e069d5.jpgfor P2 and R2, respectively.

 以下小題僅需依序寫下答案即可,不需做任何推導。


【題組】

(4.2) Let's define an inner product for P2 by ＜p(x),q(x)630835fbd3fde.jpg,for arbitrary 6308361be6402.jpgand γ≠I an undecided parameter. Find the orthonormal basis, denoted by F := [f1, f2], of P2, generated from basis E given above to satisfy the subspace equality constraints Span(f1)=Span(I) and Span(f1,f2)=Span(1,x). (8%)