活動名稱
【解題達人! We want you!】
活動說明
阿摩站上可謂臥虎藏龍，阿摩發出200萬顆鑽石號召達人們來解題!
針對一些題目可能有疑問但卻缺少討論，阿摩主動幫大家尋找最佳解!
懸賞試題多達20萬題，快看看是否有自己拿手的科目試題，一旦你的回應被選為最佳解，一題即可獲得10顆鑽石。
懸賞時間結束後，只要摩友觀看你的詳解，每次也會得到10顆鑽石喔!
關於鑽石
如何使用:
- ✔懸賞試題詳解
- ✔購買私人筆記
- ✔購買懸賞詳解
- ✔兌換VIP
(1000顆鑽石可換30天VIP) - ✔兌換現金
(50000顆鑽石可換NT$4,000)
如何獲得:
- ✔解答懸賞題目並被選為最佳解
- ✔撰寫私人筆記販售
- ✔撰寫詳解販售(必須超過10讚)
- ✔直接購買 (至站內商城選購)
** 所有鑽石收入，都會有10%的手續費用
近期考題
2.某种病菌感染人体并侵入细胞内后，机体可以对该细胞产生免疫反应，其中有
(A)效应B细胞接触靶细胞裂解，从而病菌抗原白细胞介素消灭
(B)效应B细胞接触靶细胞，导致靶细胞裂解，从而使病菌抗原被抗体消灭
(C)效应T细胞接触靶细胞，导致靶细胞裂解，从而使病菌抗原被外毒素消灭
(D)效应T细胞接触靶细胞，导致靶细胞裂解，从而使病菌抗原被抗体消灭
(A)效应B细胞接触靶细胞裂解，从而病菌抗原白细胞介素消灭
(B)效应B细胞接触靶细胞，导致靶细胞裂解，从而使病菌抗原被抗体消灭
(C)效应T细胞接触靶细胞，导致靶细胞裂解，从而使病菌抗原被外毒素消灭
(D)效应T细胞接触靶细胞，导致靶细胞裂解，从而使病菌抗原被抗体消灭
13 如果某項根據淨現值法評估之 5 年期資本預算，原始投資額為$1,000,000，在沒有通貨膨脹之考量下，淨現
值為$10,000，故公司決定進行該項資本支出。然而如果預期未來通貨膨脹率每年達 5%，請問該項資本支出 是否仍會出現正的淨現值？
(A)仍然會有正的淨現值
(B)淨現值受到通貨膨脹之影響有多大，要視計算淨現值所採用之最低報酬率而定
(C)因為不考慮通貨膨脹之投資報酬率僅為 1%，小於通貨膨脹率 5%，所以淨現值將變為負值
(D)考量通貨膨脹後，淨現值一定會變小，但是否為負值並不一定
(A)仍然會有正的淨現值
(B)淨現值受到通貨膨脹之影響有多大，要視計算淨現值所採用之最低報酬率而定
(C)因為不考慮通貨膨脹之投資報酬率僅為 1%，小於通貨膨脹率 5%，所以淨現值將變為負值
(D)考量通貨膨脹後，淨現值一定會變小，但是否為負值並不一定
【非選題】
【題組】
(B) (5%) By the above definitions and theorem, show the following statement is true or false. You should also show your reasons. If the reasons are incorrect, then you get no point. Statement: An NPC problem can polynomially reduce to any NPC problem.
1. We have the following definitions and theorem related to NP-completeness.
Definition 1. Let X1 and X2 be tow problems. X1 polynomially reduces to X2 (written as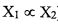 
) if and
only if X1can be solved in polynomial time, by using a polynomial time algorithm which solves X2.
Definition 2. A problem is said to be a P (resp, NP) problem if it can be solved in polynomial time by a deterministic (resp,, non-deterministio) algorithn.
Definition 3. NP (resp., P) is the set of all NP (resp., P) problems.
Definition 4. A problem X is an NP-complete (NPC) problem if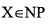
and every NP problem reduces to X.
Cook's Theorem. NP=P if and only if the satisfiability (SAT) problem is a P problem. (This implies that every NP problem polynomially reduces to SAT.)
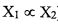) if and
only if X1can be solved in polynomial time, by using a polynomial time algorithm which solves X2.
Definition 2. A problem is said to be a P (resp, NP) problem if it can be solved in polynomial time by a deterministic (resp,, non-deterministio) algorithn.
Definition 3. NP (resp., P) is the set of all NP (resp., P) problems.
Definition 4. A problem X is an NP-complete (NPC) problem if
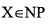and every NP problem reduces to X.Cook's Theorem. NP=P if and only if the satisfiability (SAT) problem is a P problem. (This implies that every NP problem polynomially reduces to SAT.)
【題組】
(B) (5%) By the above definitions and theorem, show the following statement is true or false. You should also show your reasons. If the reasons are incorrect, then you get no point. Statement: An NPC problem can polynomially reduce to any NPC problem.
【非選題】
【題組】(一) 初期反應：站務人員和列車司機員在事件發生的第一時間應如何反應，確保乘客的生命安全？(5 分)
三、在捷運車站或車廂內發生恐怖分子隨機傷人事件時，捷運系統的應變處理是保障乘客安全和迅速恢復運營的關鍵。請從以下幾個方面探討捷運系統在面對此類突發事件時的應變處理措施。
【題組】(一) 初期反應：站務人員和列車司機員在事件發生的第一時間應如何反應，確保乘客的生命安全？(5 分)