110年 - 110 國立中央大學_碩士班招生考試_機械工程學系/共同(一般生):自動控制#111071

1) f(t)=

.

2) f(t) = tsin 2t.

3) f(t) =.

4) f(t) t²sin 2t.

5) f(t) .

(a) Sketch the root loci for positive K values. Find the break-away points. (10 pt)

(b) Find the corresponding values of K for the break-away points. (5 pt)

(c)When the input signal R(s) is a unit step function, find the steady state error.(10 pt)

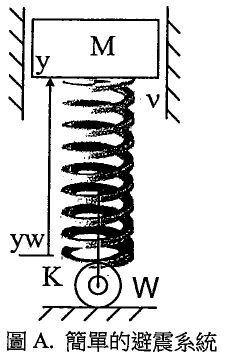
3.(25分)下圖A描述一個簡單的避震系統,包含質量M、彈簧K、與阻尼v的動態系統::質量M在垂直黏滯摩擦v的滑軌內只能上下滑動,M被頂在直彈簧上,弹簧係數為K。圖B描述了M 之受力的自由體圖:固定重力g向下、彈簧力K*(y(t)-yw(t)向下、黏滯摩擦力v*d(yt) yw(t)/dt 向下、外加施力F(0)向上,而yw為彈簧與阻尼器的被設定的繫點的相對於地面固定位置的向上垂直座標、y為M在彈頂端的位置向上垂直座標、0彈力時彈簧長度為L0。*請列出描述M的力的平衡動態方程式,是位置時間函數的時間微分方程式,請寫出其對應的拉氏域的代數方程式,別忘了包括y(t)與(d/dt)y(t)的初始值(10分) 這樣一個二階系統的動態特徵分母多項式般寫成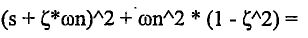為阻尼因數。 .*請問與系統元件的特性參數M、K・v之函數關係為何?(7分)*已知階梯響應的突波ovesoo比例.*若希望完全沒有突破,Mp該如何選,而為了避震系統不至於產生暈眩,只需要突波不太大,可以選擇Mp≦0.0948,如此請問應該如何選?M、K、v應該如何?(8分)

(a)當C(s)=K時,其中K為一固定正數,請此系統的穩態誤差(steady state error)為何?(5分)

(b)如(a)中選擇C(s)=K時,Y(S所對應的反應y(t)的overshoot 有多少 percent(%)?(5分)

(c)若工程師A希望降低穩態誤差,將控制器設計為C(s)=K/s時,卻發現系統有可能會不穩定,請問使得整個閉迴路系統(closed1oop system)穩定的K的範圍為何?(5分)

(d)若工程師B希望設計控制器為C(s)=K(s-z)(S-p時,且希望閉路的 poles均為2時則C(S)該如何設計?(10分)

110年 - 110 國立中央大學_碩士班招生考試_機械工程學系/共同(一般生):自動控制#111071

試卷資訊

選擇題 (0)

申論題 (13)