試題詳解

2. The linear combination of a set of vectors is an essential element in linear algebra. We say a set V is invariant under linear combination if the implication "∀n ∈ and any set of vectors {v₁, ..., 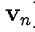} ⊂ V ⇒ the set of all linear combinations {c₁v₁ + ... + } ⊂ V" holds. And we say a mapping L defined on a set X is invariant under linear combination if the form of linear combination is unchanged under L, or more precisely the statement ", and any set of vectors {x₁, ..., } ⊂ X, the identity L(c₁x₁ + ... + ) = c₁L(x₁) + ... + holds" is true. Which one of the following statements related to linear combination is false

(A)Let S be a subset of a vector space V. Then S is a subspace of V if S is invariant under linear combination. 

(B) Let {V₁, ..., 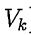} be a set of k subspaces of a vector space W and denote span{V₁, ..., } as the set of all linear combinations of the form c₁v₁ + ... + with each vᵢ chosen freely from . Then span{V₁, ..., 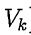} is also a subspace of W with dim(span{V₁, ..., }) = dim(V₁) + ... + dim()

 
(C) Let A and B be two matrices and denote C := AB. Then each column of C is a linear combination of all columns of A, and so rank≤ rank is implied.

(D) A mapping L between two vector spaces is a linear transformation if and only if it is invariant under linear combination.
(E) Let (V, (. ,. )ᵥ) be an inner product space. Then (. , .)ᵥ is invariant under linear combination at either one of its two arguments.