2. The linear combination of a set of vectors is an essential element in linear algebra. We say a set V is invariant under linear combination if the implication "∀n ∈  and any set of vectors {v₁, ...,
and any set of vectors {v₁, ..., 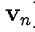 } ⊂ V ⇒ the set of all linear combinations {c₁v₁ + ... +
} ⊂ V ⇒ the set of all linear combinations {c₁v₁ + ... +  } ⊂ V" holds. And we say a mapping L defined on a set X is invariant under linear combination if the form of linear combination is unchanged under L, or more precisely the statement "
} ⊂ V" holds. And we say a mapping L defined on a set X is invariant under linear combination if the form of linear combination is unchanged under L, or more precisely the statement " , and any set of vectors {x₁, ...,
, and any set of vectors {x₁, ...,  } ⊂ X, the identity L(c₁x₁ + ... +
} ⊂ X, the identity L(c₁x₁ + ... +  ) = c₁L(x₁) + ... +
) = c₁L(x₁) + ... +  holds" is true. Which one of the following statements related to linear combination is false
holds" is true. Which one of the following statements related to linear combination is false
(A)Let S be a subset of a vector space V. Then S is a subspace of V if S is invariant under linear combination.
(B) Let {V₁, ..., 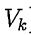 } be a set of k subspaces of a vector space W and denote span{V₁, ...,
} be a set of k subspaces of a vector space W and denote span{V₁, ...,  } as the set of all linear combinations of the form c₁v₁ + ... +
} as the set of all linear combinations of the form c₁v₁ + ... +  with each vᵢ chosen freely from
with each vᵢ chosen freely from  . Then span{V₁, ...,
. Then span{V₁, ..., 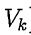 } is also a subspace of W with dim(span{V₁, ...,
} is also a subspace of W with dim(span{V₁, ...,  }) = dim(V₁) + ... + dim(
}) = dim(V₁) + ... + dim( )
)
(C) Let A and B be two matrices and denote C := AB. Then each column of C is a linear combination of all columns of A, and so rank ≤ rank
≤ rank is implied.
is implied.
(D) A mapping L between two vector spaces is a linear transformation if and only if it is invariant under linear combination. (E) Let (V, (. ,. )ᵥ) be an inner product space. Then (. , .)ᵥ is invariant under linear combination at either one of its two arguments.