複選題

17. The linear independence is without doubt one of the most important concepts in linear algebra. Which of the following statements about this concept are true?
(A) The number of linearly independent columns of any matrix is equal to the number of linearly independent rows of the matrix.
(B) A set of vectors {v₁, ..., 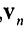} is linearly independent if there exist coefficients c₁, ..., , all of them are zero, such that c₁v₁ + ... + = 0.
(C) The linear independence of a set of vectors is a necessary but not sufficient condition for them to be a basis of a vector space.
(D) A square matrix is diagonalizable if and only if all its eigenvectors are linearly independent.
(E) Let (λ₁, x₁) be the i th eigenvalue-eigenvector-pair of a square matrix. Then all λ's are distinct if and only if the set {x₁, ..., } of eigenvectors is linearly independent.

1. When using the Gaussian elimination to solve a linear equation Ax = b, elementary row operations (or multiplication by elementary matrices) are applied to the augmented matrix [A b]. Actually, there are many places in linear algebra where such a technique plays its role； e.g., the null space of A can be determined by setting b = 0. Which of the following cannot be determined by applying such a technique? (A) the range of A (B) the inverse of A (if it is nonsingular) (C) the QR factorization of A (D) the LU factorization of A (if it is square) (E) the determinant of A (if it is square).

2. The linear combination of a set of vectors is an essential element in linear algebra. We say a set V is invariant under linear combination if the implication "∀n ∈ and any set of vectors {v₁, ..., } ⊂ V ⇒ the set of all linear combinations {c₁v₁ + ... + } ⊂ V" holds. And we say a mapping L defined on a set X is invariant under linear combination if the form of linear combination is unchanged under L, or more precisely the statement ", and any set of vectors {x₁, ..., } ⊂ X, the identity L(c₁x₁ + ... + ) = c₁L(x₁) + ... + holds" is true. Which one of the following statements related to linear combination is false (A)Let S be a subset of a vector space V. Then S is a subspace of V if S is invariant under linear combination.  (B) Let {V₁, ..., } be a set of k subspaces of a vector space W and denote span{V₁, ..., } as the set of all linear combinations of the form c₁v₁ + ... + with each vᵢ chosen freely from . Then span{V₁, ..., } is also a subspace of W with dim(span{V₁, ..., }) = dim(V₁) + ... + dim()  (C) Let A and B be two matrices and denote C := AB. Then each column of C is a linear combination of all columns of A, and so rank≤ rank is implied. (D) A mapping L between two vector spaces is a linear transformation if and only if it is invariant under linear combination. (E) Let (V, (. ,. )ᵥ) be an inner product space. Then (. , .)ᵥ is invariant under linear combination at either one of its two arguments.

3. Consider the system represented by the differential equation ẍ+ẍ+kx. Which of the following is true? (A) the system is critically damped when k = 1 (B) the system is underdamped when k = 1/2 (C) the system is overdamped when k = 0.3 (D) the damping ratio of the system is increased when increasing k (E) none of the above

4. Consider the differential equation ẍ + bẋ + kx = cos(ωt) and its sinusoidal solution . Which of the following is true? (A) for a fixed b, the amplitude of is maximized when k = ω² (B) for a fixed b, the maximal amplitude of is 1/b (C) for fixed b and k, the amplitude of always grows as ω increases (D) the period of is 2πω (E) the period of depends on b and k.

5. Consider the differential equation tẋ + x = cos(ωt). Which of the following is true? (A) the general solution is sin(ωt) + C, C is a constant. (B) the particular (forced) solution is periodic with period ω (C) the solution is NOT bounded when t grows to infinity (D) If x(π/ω) = 1, then the solution is (sin(ωt) + π)/(ωt) (E) none of the above

複選題6. Consider a system whose dynamics is governed by a linear constant-coefficient ODE. Suppose the impulse response of this system is . Which of the following is true? (A) the system is order (B) the characteristic equation of the system has a pair of complex roots (C) the unit step response has oscillatory behavior (D) the unit step response does NOT converge to a constant value (E) the unit step response is equal to /3

7. Consider the heat equation , ∀0 ＜ x ＜ 1, t ＞ 0 u(0,t) = u(1,t) = 0 ∀t ＞ 0 u(x, 0) = f(x), ∀0 ＜ x ＜ 1 (A) the heat equation is nonlinear (B) without considering the boundary condition, the general solution is (C) suppose f(x) = 7 sin(3x), then the solution is u(x,t) = (D) all of the above are true (E) none of the above is true

8. Define the del operator ∇ := (A) ∇(∇ × F) = 0, where F is a vector field with continuous first and second derivatives. (B) ∇(F × G) = G ⋅ (∇ × F) – F ⋅ (∇ × G), where F and G are two smooth vector fields (C) ∇ ⋅ (φF) = ∇φ ⋅ F + (∇ ⋅ F), where φ is a smooth scalar field and F a smooth vector field. (D) all of the above are true (E) none of the above is true

9. The Fourier transform of the function f(t) = u(t-2) is F(jω) = e＜sup＞aω (b+jc), where u(t) is an unit-step function. Then which of the following statements is correct? (A) a=-2, b=1, c=0. (B) a = 2, b =1, c=0. (C) a＞0, b＞1, c=0. (D) a＜2, b≠1, c≠0. (E) None of the above statements are correct.

10. Given that f(t) has the Fourier transform F(jω). Let f1(t) = f(-3t-6), and let the Fourier transform of f1(t) be F₁(jω) = . Then which of the following statements is correct? (A) a=3, b=3, c=2. (B) 0＜a＜1, -1＜b＜0, 0＜c≤2. (C) a = -3, b=1/3, c=3. (D) a＞0, b＞0, c＜0. (E) None of the above statements are correct.

109年 - 109 國立中山大學_碩士班招生考試_電機(甲、戊、己組)、通訊所(乙組)、電波聯合：工程數學甲#106080

107年 - 107 國立中山大學_碩士班招生考試_電機系(甲、己組)、電波領域：工程數學甲#110523

106年 - 106 國立中山大學_碩士班招生考試_電機系(甲、己組)、電波領域：工程數學甲#125264

104年 - 104 國立中山大學_碩士班招生考試_電機系(甲組、丁組、己組)：工程數學甲#110231

103年 - 103 國立中山大學_碩士班招生考試_電機系(甲、丁、戊、己組)：工程數學甲#110234

102年 - 102 國立中山大學_碩士班招生考試_電機系(甲、丙、丁、戊、己組)：工程數學甲#110510