申論題

4.(25%) Let P₂ denote the vector space of all polynomials of degree less than 2. (Consider the transformation L:P₂ →R² defined by L(p(x)): =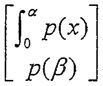 with  undecided parameters a＞0 and 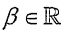. Let A be the matrix representation of transformation L with respect to the ordered bases E = [I, x] and E'= 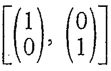for P₂ and R², respectively.

 以下小題僅需依序寫下答案即可,不需做任何推導。

(4.2) Let's define an inner product for P₂ by ＜p(x),q(x),for arbitrary and γ≠I an undecided parameter. Find the orthonormal basis, denoted by F := [f₁, f₂], of P₂, generated from basis E given above to satisfy the subspace equality constraints Span(f₁)=Span(I) and Span(f₁,f₂)=Span(1,x). (8%)