申論題

3.(11%)下面的問题共有二個子題,(1)子題要清楚地寫山證明,(b)子題只要簡短扼要地回答 提問即可。 Let A be any matrix in 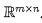. Then, since rank(A) = dim(R(A)), the dimension of range of A, and R(A) = R(AA^T), we have the result rank(A) = rank(AA^T). Therefore, when replacing A by its QR factorization, we get rank(A) = rank(QRR^TQ^T).

(a) (6%) Please continue the argument to derive the result rank(A) = rank(R).
(接下來前段是背景知識介紹,之後才是提問)Insthq given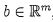, instead of using the elementary row operations (i.e. the Gauss eliminations) to manipulate the equation, we may also apply the QR factorization to the equation to get QRx = b, which implies further Q^T QRx = Q^Tb. Since Q^TQ = _In, it gives Rx = Q^Tb. Thus, according to the result of (a), when all columns of A are linearly independent, the square matrix R is nonsingular and so the solution x =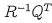b is obtained. It seems that we may summarize the above argument as the following statement: 

Given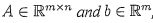, where all columns of A are assumed linearly independent, then solution to the equation Ax = 6 can always be computed from x =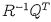, where Q and R are matrices obtained from the QR factorization of A.

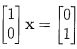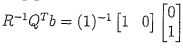 However, the simple example shows that the summary is incorrect because, according to the summary, the solution is x ==0 and obviously it does not satisfy the original equation.