二、如下圖,A、B、C 三點位於同一直線上, X=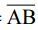 、 Y=
、 Y=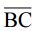 為兩段待求
距離,今獨立觀測兩線段a =
為兩段待求
距離,今獨立觀測兩線段a =  及b =
及b = 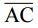 ,誤差分別為σ 及2σ :
,誤差分別為σ 及2σ :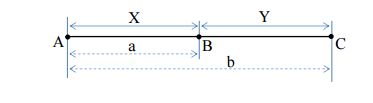
1.推算該距離的最或是值
精度不等表示不等權,而且它只有重複觀測一段距離,即表示其只有一個未知數,故採直接觀測平差法來推算該距離的最或是值。
假設重複觀測距離n次,則有n個觀測量,設觀測量為li(i=1,2,3,4,5,6.....),且觀測量的權為Pi(i=1,2,3,4,5,6.....),其最或是值可以寫成ΣPi*li/ΣPi,推導如下:
令最或是值=X
觀測方程式:li+Vi=X
改正數方程式:Vi=X-li
令φ=[PVV],因誤差平方和[PVV]要最小,因此:
φ=P1V12+P2V22+P3V32+P4V42+P5V52+......+PiVi2→min(最小值)
φ=P1(X-l1)2+P2(X-l2)2+P3(X-l3)2+P4(X-l4)2+P5(X-l5)2+......+Pi(X-l6)2→min(最小值)
令其為0,做偏微分:
∂φ/∂X=2P1(X-l1)+2P2(X-l2)+.......+2Pi(X-li)=0
最或是值X=(P1l1+P2l2+.......+Pili)/(P1+P2+......+Pi)=ΣPi*li/ΣPi
2.評定該最或是值的精度
先算單位權中誤差(σ=√[PVV]/(n-1)),再進一步得出最或是值中誤差(σx=σ/√ΣPi)及每個觀測值得中誤差(σi=σ/√Pi)。