申論題

三、計算證明題
1. 閱讀以下文章並回答下面問題：（上面題目的性質或解答即使無法證明，依然可以用來解下面的問題，但反之不行。）
九連環是一種源於中國傳統的智力遊戲。這玩具由兩個主要部份構成：一部分為「九個環」，另一部分為一把「劍」，遊戲目標是把九個圓環全部套上或全部卸下。右圖為九個圓環全部套上的示意圖。每個環有兩種狀態，一個是被劍穿過（掛在劍上）， 一個是與劍分離。每次改變一個環的狀態稱作一步。但不是任意的環都能改變狀態， 必須符合下列兩種條件之一（依右圖的左右方向）才能改變狀態：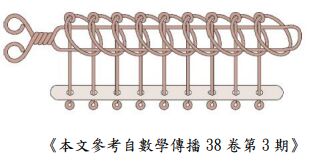

（R）最右邊的環
（S）劍上最右邊環之左邊的環
解法：我們給出一個數學模型如下
令 1 表示環在劍上，用 0 表示環不在劍上，而九個環的狀態就寫成一個 9 位的二進位數。而這兩種操作方式R與S視為狀態函數。
舉例來說： R(101011100₂)=101011101₂或S(101011100₂)=101010100₂。遊戲過程中只要不斷的操作R與S ，我們就一定能夠將111111111₂ 變為000000000₂