題組內容
一、欲研究兒童體重(WGT)與身高(HGT)和年齡(AGE)之關係對某種營養不良症
狀的影響。考慮反應變數y = WGT,而解釋變數則為x1 = HGT和x2 = AGE,且以最小
平方法(least square method)配適模型 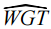 = 3.438 + 0.724HGT + 2.777AGE - 0.042(AGE)2
及 ANOVA(analysis of variance)表如下:
= 3.438 + 0.724HGT + 2.777AGE - 0.042(AGE)2
及 ANOVA(analysis of variance)表如下: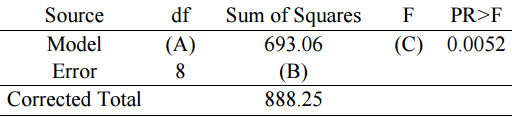
WGT = β0 +β1HGT +β2AGE +β3(AGE)2
+ Error.
若有 12 個兒童參與臨床試驗,並得配適模型(fitted model)
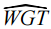 = 3.438 + 0.724HGT + 2.777AGE - 0.042(AGE)2
及 ANOVA(analysis of variance)表如下:
= 3.438 + 0.724HGT + 2.777AGE - 0.042(AGE)2
及 ANOVA(analysis of variance)表如下: