題組內容

4.下圖 6 中，ABCD 為四連桿之曲柄搖桿機構，桿件 AB 長度為 e，桿件 BC 長度為 f，桿件 CD 長度為 g，桿件 AD 長度為 h，請回答下列各點：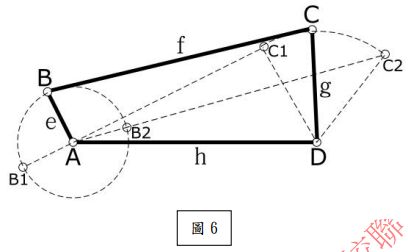

(2)請列式證明該桿件長度為最短。（15％）

詳解提供者：Felix J 謝謝阿摩已上岸

格拉霍夫定律（Grashof's Law）
- 要判斷一個四連桿機構是否為曲柄搖桿機構，需要應用格拉霍夫定律。
- 格拉霍夫定律的公式為：S + L ≤ P + Q
  - S：最短桿的長度
  - L：最長桿的長度
  - P、Q：其餘兩桿的長度
- 並且要形成曲柄搖桿機構，最短桿必須要能完整旋轉，所以最短桿的長度必須符合以下條件。
- 最短桿 + 最長桿 <= 其餘兩桿相加
- 並且最短桿為曲柄，與最短桿相連的桿件其中之一為機架。
證明過程：
- 在圖 6 的四連桿機構中，要構成曲柄搖桿機構，必須滿足以下條件：
  - 最短桿（e）+ 最長桿（假設為 h）≤ 其餘兩桿（f + g）
  - e + h ≤ f + g
- 如果 e 是最短桿，並且滿足上述條件，則該機構為曲柄搖桿機構。
重點說明：
- 格拉霍夫定律是判斷四連桿機構類型的重要依據。
- 在曲柄搖桿機構中，最短桿通常是曲柄，能夠完整旋轉。
- 實際應用中，可以通過測量桿件長度，並代入格拉霍夫定律公式進行驗證。