題組內容

四、已知一連續線性控制系統方程式如下：
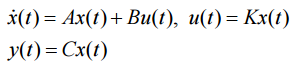
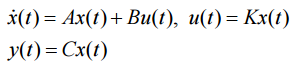
其中 x ∈ R n×1 為系統狀態， A ∈ R n×n ， B ∈ R n×m ， C ∈ R l×n 為系統矩陣， K ∈ R m×n 為控 制器增益， y ∈ R l×1 為系統輸出。

⑶對偶原理（duality）是否亦存在於連續最佳化理論？請說明。（5 分）

詳解 (共 1 筆)

詳解 提供者：hchungw

是的，對偶原理（duality）在連續最佳化理論中確實存在。在最佳化問題中，對偶性是一個重要的概念，特別是對於線性和凸最佳化問題。

對偶原理基本上說明了每一個最佳化問題（稱為原始問題）都有一個相對應的對偶問題。對於某些特定類型的問題，對偶問題提供了原始問題的下界，而在某些條件下（例如當滿足強對偶性時），原始問題和對偶問題的解會相等。

這種對偶性在許多應用中都是非常有用的，例如：

  1. 演算法設計：一些問題可能在其對偶形式下更容易解決。
  2. 敏感度分析：了解如何更改問題參數會影響最佳解。
  3. 理論洞察：通過對偶性，我們可以更好地理解問題的結構和性質。

在連續最佳化中，對偶性主要用於凸優化問題，因為在這種情況下，它提供了豐富的理論結果和明確的關係。但是，它也可以擴展到其他類型的最佳化問題。