6.人在說話、打噴嚏和咳嗽時,會產生飛沫,台灣衛生福利部某篇文章說飛沫可存在空中幾小時,而 COVID-19 是由新型冠狀病毒經過飛沫、直接或間接接觸帶有病毒的分泌物傳染,因此小東想要用物理概念來確認飛沫在空中的停留時間,便開始飛沫的探究歷程。小東考慮『飛沫在距離地面高度 1.8 公尺處,由靜止開始落下』的情境下,去分析飛沫運動情況。首先,小東分析飛沫落下時,會受到重力和空氣造成的阻力作用,飛沫會先變速率運動,最後再等速度運動。接著,小東從網路查資料,知道飛沫的可以視為密度為 1 公克/立方公分的球,它的半徑範圍大約在 0.1 微米到 2 毫米,半徑會影響空氣造成的阻力。若空氣密度約為 1.2 公斤/立方公尺,空氣黏滯係數η約為 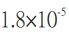 牛頓•秒/平方公尺,當飛沫的半徑為 r 公尺、速率為 v公尺/秒時,飛沫受到空氣阻力主要可分為兩種情況:
牛頓•秒/平方公尺,當飛沫的半徑為 r 公尺、速率為 v公尺/秒時,飛沫受到空氣阻力主要可分為兩種情況:
A、半徑很小時(r≤ 100微米),斯托克斯提出阻力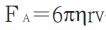 牛頓。小東利用這個阻力去分析 飛沫運動,飛沫可以忽略變速率運動,整體近似為等速度運動。
牛頓。小東利用這個阻力去分析 飛沫運動,飛沫可以忽略變速率運動,整體近似為等速度運動。
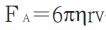 牛頓。小東利用這個阻力去分析 飛沫運動,飛沫可以忽略變速率運動,整體近似為等速度運動。
牛頓。小東利用這個阻力去分析 飛沫運動,飛沫可以忽略變速率運動,整體近似為等速度運動。 B、半徑很大時(r≥1000微米),瑞利提出阻力 牛頓。小東利用這個阻力去分析 飛沫運動,飛沫受到阻力造成影響可以忽略。
牛頓。小東利用這個阻力去分析 飛沫運動,飛沫受到阻力造成影響可以忽略。
已知重力加速度量值為g=10公尺/秒2,試根據以上敘述,完成飛沫半徑與落地時間關係表:

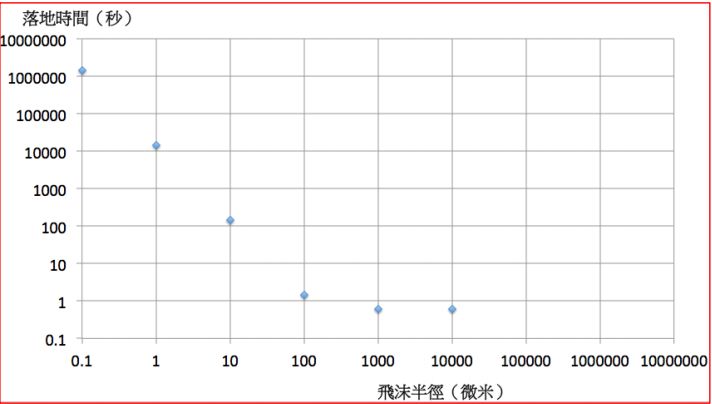
根據飛沫半徑與落地時間關係表,且半徑為操作變因,落地時間為應變變因,畫出飛沫半徑與落地時間的關係圖。(請注意科學繪圖需要注意的地方,且此圖為對數圖)
 牛頓。小東利用這個阻力去分析 飛沫運動,飛沫受到阻力造成影響可以忽略。
牛頓。小東利用這個阻力去分析 飛沫運動,飛沫受到阻力造成影響可以忽略。已知重力加速度量值為g=10公尺/秒2,試根據以上敘述,完成飛沫半徑與落地時間關係表:

根據飛沫半徑與落地時間關係表,且半徑為操作變因,落地時間為應變變因,畫出飛沫半徑與落地時間的關係圖。(請注意科學繪圖需要注意的地方,且此圖為對數圖)