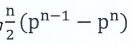
43. 已知投擲某枚硬幣,已知出現正面的機率為p,出現反面的機率為(1-p)。現投擲此硬幣n次,在投擲的過程中,第一次正面出現時,可獲得1元,第二次正面出現時,可再獲得2元,第三次正面出現時,可再獲得3元,依此類推。請問下列敘述何者正確? (A)總共得到(n²-n)元的機率為 (B)投擲硬幣第二次之後,累計獲得1元的機率為2(p-p²) (C)若n次投擲中出現正面r次,總共可拿到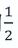(r²-r)元 (D)若n次投擲後累計獲得3元,其機率為