申論題 - 阿摩線上測驗

申論題資訊

試卷：101年 - 台中教育大學101年師資生及教育學程甄選數學試題#57262
科目：教甄◆數學
年份：101年
排序：0

11.如下圖， △ABC 中， ∠A 的外角為 134°，∠B 和 ∠C 的內角平分線相交於 I 點， ∠B 的內角平分線和 ∠C 的外角平分線相交於 P 點，求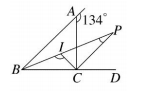： phpkdc4CB

(1) ∠BIC =____________度；

詳解提供者：IU

荳爸國一上 (2016/11/28 13:24): 0
∠BIC = 180 - 1/2 * (∠ABC + ∠ACB) = 180 - 1/2 * 134 = 180-67=113°

詳解提供者：莊東凌

A: 113度

詳解提供者：Frank Wu

113度

詳解提供者：kkppff

設∠ABI=X°=∠IBC，∠ACI=Y°=∠ICB ∠ABC+∠ACB=134°=2X+2Y，所以X+Y=67° 在△IBC中，∠I的外角∠PIC=∠IBC+∠ICB=X+Y=67° 所以∠BIC=180°-67°=113°

詳解提供者：雅婷

∠A=180-134=46 ∠B+∠C=134 因為∠B 和 ∠C 的內角平分線相交於 I 點 ∠IBC+∠ICB=134÷２＝67 ∠BIC=180-67=113

詳解提供者：林宏銘

113

詳解提供者：彥涵

134/2=67 180-67=113=角I

詳解提供者：Wenny

113

詳解提供者：Yi-Ting Chen

113

詳解提供者：荳爸

∠BIC = 180 - 1/2 * (∠ABC + ∠ACB) = 180 - 1/2 * 134 = 123°